Chapter 3.2. Simple Conditions – Exam Problems
In the previous chapter, we went through the simple conditional statements in JavaScript, which we can use to execute different actions depending on a given condition. We mentioned what is the scope of a variable (it's scope) and how to track the execution of our program step by step (the so-called debugging). In this chapter, working with simple conditions by going through some exam tasks. To do this, let's first revise their construction:
if (bool expression) {
// condition body;
} else {
// else-construction body;
}
if conditions consist of:
ifclause- bool expression - a variable of bool type (
Boolean) or bool logical expression (an expression that results intrue/false) - condition body - contains a random block of source code
elseclause and its block of source code (optional)
Exam Problems
After having revised how to write simple conditions, let's solve a few exam problems to practice the if-else construction:
Problem: Transport Price
A student has to travel n kilometers. He can choose between three types of transportation:
- Taxi. Starting fee: 0.70 BGN. Day rate: 0.79 BGN/km. Night rate: 0.90 BGN/km.
- Bus. Day / Night rate: 0.09 BGN/km. Can be used for distances of a minimum of 20 km.
- Train. Day / Night rate: 0.06 BGN/km. Can be used for distances of a minimum of 100 km.
Write a program that reads the number of kilometers n and period of the day (day or night) and calculates the price for the cheapest transport.
Input Data
Two lines (arguments) are read from the console:
- The first line (arguments) contains a number n – number of kilometers – an integer in the range of [1 … 5000].
- The second line contains the word "day" or "night" – traveling during the day or the night.
Output Data
Print on the console the lowest price for the given number of kilometers.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 5 day |
4.65 | 7 night |
7 |
| Input | Output | Input | Output |
|---|---|---|---|
| 25 day |
2.25 | 180 night |
10.8 |
Hints and Guidelines
We will read the input data and depending on the distance, we will choose the cheapest transport. To do that, we will write a few conditional statements.
Processing The Input Data
In the task, we are given information about the input and output data. Therefore, the first part of the task is to declare and initialize two variables where we will store the values of the input data:
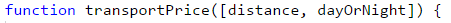
Before starting with the conditional statements, we need to declare one more variable that stores the value of the transport price:
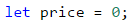
Checking The Conditions and Calculating
After having declared and initialized the input data and the variable that stores the value of the price, we have to decide which conditions of the task have to be checked first.
The task specifies that the rates of two of the vehicles do not depend on whether it is day or night, but the rate of one of the transports (taxi) depends. This is why the first condition will be whether it is day or night so that it is clear which rate the taxi will be using. To do that, we declare one more variable that stores the value of the taxi rate:
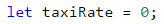
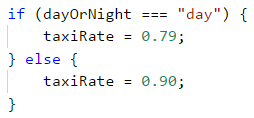
To calculate the taxi rate, we will use a conditional statement of type if-else:
After having done that, now we can start calculating the transport price itself. The constraints in the task refer to the distance that the student wants to travel. This is why, we will use an if-else statement that will help us find the price of the transport, depending on the given kilometers:

First, we check whether the kilometers are less than 20, as the task specifies that the student can only use a taxi for less than 20 kilometers. If the condition is true (returns true), the variable that is created to store the value of the transport (price), will store the corresponding value. This value equals the starting fee that we will sum with its rate, multiplied by the distance that the student has to travel.
If the condition of the variable is not true (returns false), the next step of our program is to check whether the kilometers are less than 100. We do that because the task specifies that in this range, a bus can be used as well. The price per kilometer of a bus is cheaper than a taxi one. Therefore, if the result of the condition is true, we store a value, equal to the result of the multiplication of the rate of the bus by the distance to the variable for the transportation price in the else if statement body.
If this condition does not return true as a result, we have to store a value, equal to the result of the multiplication of the distance by the train rate to the price variable in the else body. This is done because the train is the cheapest transport for the given distance.
Printing The Output
After we have checked the distance conditions and we have calculated the price of the cheapest transport, we have to print it. The task does not specify how to format the result, therefore, we just print the variable:
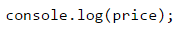
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/930#0.
Problem: Pipes In Pool
A pool with volume V fills up via two pipes. Each pipe has a certain flow rate (the liters of water, flowing through a pipe for an hour). A worker starts the pipes simultaneously and goes out for N hours. Write a program that finds the state of the pool the moment the worker comes back.
Input Data
Four numbers are passed to the function (arguments):
- The first line (argument) contains a number V – the volume of the pool in liters – an integer in the range of [1 … 10000].
- The second line (argument) contains a number P1 – the flow rate of the first pipe per hour – an integer in the range of [1 … 5000].
- The third line (argument) contains a number P2 – the flow rate of the second pipe per hour – an integer in the range of [1 … 5000].
- The fourth line (argument) contains a number H – the hours that the worker is absent – a floating-point number in the range of [1.0 … 24.00].
Output Data
Print on the console one of the two possible states:
To what extent the pool has filled up and how many percent each pipe has contributed. All percent values must be formatted to an integer (without rounding).
- "The pool is [x]% full. Pipe 1: [y]%. Pipe 2: [z]%."
- If the pool has overflown – with how many liters it has overflown for the given time – a floating-point number.
- "For [x] hours the pool overflows with [y] liters."
Have in mind that due to the rounding to an integer, there is data loss and it is normal for the sum of the percents to be 99%, not 100%.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 1000 100 120 3 |
The pool is 66% full. Pipe 1: 45%. Pipe 2: 54%. | 100 100 100 2.5 |
For 2.5 hours the pool overflows with 400 liters. |
Hints and Guidelines
To solve the task, we read the input data, write a few conditional statements, do some calculations and print the result.
Processing The Input Data
Our first step is to read the input data:
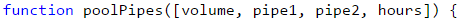
Our next step is to declare and initialize a variable in which we are going to calculate how many liters the pool has filled up for the time the worker was absent. We do the calculations by summing the values of the flow rates of the two pipes and multiplying them by the hours that are given as input data:

Checking The Conditions and Processing Output Data
After we have the value of the quantity of water that has flown through the pipes, the next step is to compare that quantity with the volume of the pool itself.
We do that with a simple if-else statement, where the condition will be whether the quantity of water is less than the volume of the pool. If the statement returns true, we have to print one line that contains the ratio between the quantity of water that has flown through the pipes and the volume of the pool, as well as the ratio of the quantity of the water from each pipe to the volume of the pool.
The ratio has to be in percentage, that is why all the calculations so far will be multiplied by 100. The values will be printed using placeholders, and as there is a condition for the result in percentage to be formatted to two digits after the decimal point without rounding, we will use the method Math.trunc(…):
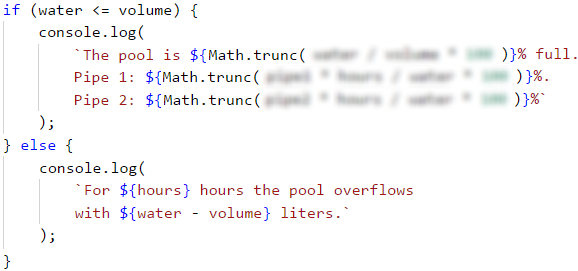
However, if the condition returns false, that means that the quantity of water is more than the volume of the pool, therefore, it has overflown. Again, the output data has to be on one line, but this time it should contain only two values – one of the hours when the worker was absent, and the quantity of water, which is the difference between *the incoming water and the volume of the pool.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/930#1.
Problem: Sleepy Tom Cat
Tom Cat likes to sleep all day but, unfortunately, his owner is always playing with him whenever he has free time. To sleep well, the norm of games that Tom has is 30 000 minutes per year. The time for games he has depends on the holidays that his owner has:
- During workdays, his owner plays with him 63 minutes per day.
- During holidays, his owner plays with him 127 minutes per day.
Write a program that reads the number of holidays and prints whether Tom can sleep well and how much the difference from the norm for the current year is. It is assumed that there are 365 days in one year.
Example: 20 holidays -> the working days are 345 (365 - 20 = 345). The time for games is 24 275 minutes (345 * 63 + 20 * 127). The difference from the norm is 5 725 minutes (30 000 – 24 275 = 5 725) or 95 hours and 25 minutes.
Input Data
The input is read from the console and consists of an integer – the number of holidays in the range of [0 … 365].
Output Data
Two lines have to be printed on the console:
- If Tom's time for games is above the norm for the current year:
- On the first line print: “Tom will run away”.
- On the second line print the difference from the norm in the format:
“{H} hours and {M} minutes more for play”.
- If the time for games of Tom is below the norm for the current year:
- On the first line print: “Tom sleeps well”.
- On the second line print the difference from the norm in the format:
“{H} hours and {M} minutes less for play”.
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 20 | Tom sleeps well 95 hours and 25 minutes less for play |
113 | Tom will run away 3 hours and 47 minutes more for play |
Hints and Guidelines
To solve the problem, we will read the input data. Then, we will write a few conditional statements and do some calculations. Finally, we will print the result.
Reading The Input Data and Calculating
From the task, we see that the input data will be an integer in the range of [0 … 365].
To solve the problem, first, we have to calculate the total minutes the owner of Tom is playing with him. We see that not only does the sleepy cat has to play with his owner during the holidays, but also during the working days. The number that we read from the console refers to the holidays.
Out next step is to calculate, with the help of that number, how many the working days of the owner are, as without them we cannot calculate the total minutes for play. As the total number of days per year is 365 and the number of holidays is X, that means that the number of working days is 365 - X*. We store the difference in a new variable that only stores this value:
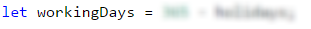
Once we have the number of days for playing, we can calculate the time for games of Tom in minutes. Its value is equal to the result of the multiplication of the working days by 63 minutes (the task specifies that during working days, the time for play is 63 minutes per day), summed with the result of the multiplication of the holidays by 127 minutes (the task specifies that during holidays, the time for play is 127 minutes per day).

In the task condition, we see that we have to print the difference between the two values in hours and minutes as output data. That is why we subtract the total time for play from the norm of 30 000 minutes and store the result in a new variable. After that, we divide that variable by 60 to get the hours, and then, to find out how many the minutes are, we use modular division with the operator %, as again we divide the variable of the difference by 60.
Here we have to note that if the total time for the playing of Tom is less than 30,000 when subtracting the norm from it, we will obtain a negative number. To neutralize the number in the division, we use the method Math.abs(…) when finding the difference:

Checking The Conditions
The time for games is already calculated, which leads us to the next step – comparing the time for play of Tom with the norm on which the good sleep of the cat depends. To do so, we will use an if-else conditional statement. In the if clause we will check whether the time for play is more than 30 000 (the norm).
Processing the Output Data
Whatever the result of the conditional statement is, we have to print how much the difference in hours and minutes is. We will do that with a placeholder and the variables that store the values of the hours and the minutes, as the formatting will be according to the task requirements for output.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/930#2.
Problem: Harvest
In a vineyard with an area of X square meters, 40% of the harvest goes for wine production. Y kilograms of grapes are extracted from a 1 square meters vineyard. 2,5 kg of grapes is needed for 1 liter of wine. The wanted quantity of wine for sale is Z liters.
Write a program that calculates how much wine can be produced and whether that quantity is enough. If it is enough, the rest is divided between the vineyard workers equally.
Input Data
The input data consists of exactly 4 lines (arguments):
- First line (argument): X square meters is the vineyard size – an integer in the range of [10 … 5000].
- Second line (argument): Y grapes for one square meters – an integer in the range of [0.00 … 10.00].
- Third line (argument): Z needed liters of wine – an integer in the range of [10 … 600].
- Fourth line (argument): number of workers – an integer in the range of [1 … 20].
Output Data
The following has to be printed on the console:
- If the produced wine is less than the needed quantity:
- “It will be a tough winter! More {insufficient wine} liters wine needed.”
* The result has to be rounded down to the nearest integer.
- “It will be a tough winter! More {insufficient wine} liters wine needed.”
- If the produced wine is more than the needed quantity:
- “Good harvest this year! Total wine: {total wine} liters.”
* The result has to be rounded down to the nearest integer. - “{Wine left} liters left -> {wine for one worker} liters per person.”
* Both of the results have to be rounded up to the higher integer.
- “Good harvest this year! Total wine: {total wine} liters.”
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 650 2 175 3 |
Good harvest this year! Total wine: 208 liters. 33 liters left -> 11 liters per person. |
1020 1.5 425 4 |
It will be a tough winter! More 180 liters wine needed. |
Hints and Guidelines
To solve the problem, we will read the input data. Then, we will write a few conditional statements and do some calculations. Finally, we will print the result.
Processing The Input Data and Performing The Calculations
First, we have to read the input data:
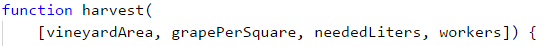
To solve the problem, based on the input data, we have to calculate how many liters of wine will be produced. From the task requirements, we see that to calculate the quantity of wine in liters, we first, have to find the number of grapes in kilograms, which we will get from the harvest. For that, we will declare a variable that keeps a value, equal to 40% of the result from the multiplication of the vineyard area by the number of grapes, which is extracted from 1 .
After having done these calculations, we are ready to calculate the quantity of wine in liters that will be produced from the harvest as well. For that, we declare one more variable that stores that quantity. To calculate, we have to divide the number of grapes in kg by 2.5:

Checking The Conditions and Processing Output Data
After having done the necessary calculations, the next step is to check whether the liters of wine that have been produced, are enough. For that, we will use a simple conditional statement of the if-else type and we will check whether the liters of wine from the harvest are more than or equal to the needed liters.
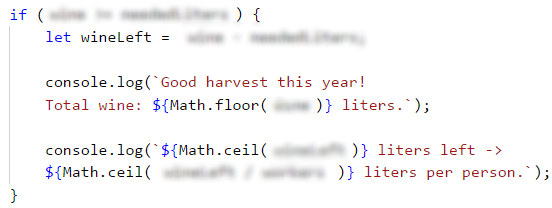
If the condition returns true, from the task requirement we see that on the first line we have to print the wine that has been produced from the harvest. That value has to be rounded down to the nearest integer, which we will do by using both the method Math.floor(…) and a placeholder when printing it.
On the second line, we have to print the results by rounding them up to the higher integer, which we will do by using the method Math.ceil(…). The values that we have to print are the quantity of wine left and the quantity that each worker gets. The wine left is equal to the difference between the produced liters of wine and the needed liters of wine.
We calculate the value of that quantity in a new variable, which we declare and initialize in the if condition body, before printing the first line. We calculate the quantity of wine that each worker gets by dividing the wine left by the number of workers.
If the condition returns false, we have to print the difference between the needed liters and the liters of wine produced from the harvest. There is a specification that the result has to be rounded down to the nearest integer, which we will do by using the method Math.floor(…).

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/930#3.
Problem: Firm
A firm gets a request for creating a project for which a certain number of hours are needed. The firm has a certain number of days. During 10% of the days, the workers are being trained and cannot work on the project. A normal working day is 8 hours long. The project is important for the firm and every worker must work on it with overtime of 2 hours per day.
The hours must be rounded down to the nearest integer (for example, 6.98 hours are rounded to 6 hours).
Write a program that calculates whether the firm can finish the project on time and how many hours more are needed or left.
Input Data
The input data contains exactly three lines (arguments):
- On the first line (argument) are the needed hours – an integer in the range of [0 … 200 000].
- On the second line (argument) are the days that the firm has – an integer in the range of [0 … 20 000].
- On the third line (argument) are the number of all workers – an integer in the range of [0 … 200].
Output Data
Print one line on the console:
- If the time is enough:
- "Yes!{the hours left} hours left."
- If the time is NOT enough:
- "Not enough time!{additional hours} hours needed."
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 90 7 3 |
Yes!99 hours left. | 99 3 1 |
Not enough time!72 hours needed. |
Hints and Guidelines
To solve the problem, we will read the input data. Then, we will write a few conditional statements and do some calculations. Finally, we will print the result.
Reading The Input Data
First, we have to read the input data to solve the problem.
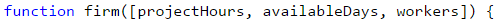
Auxiliary Calculations
The next step is to calculate the number of total working hours by multiplying the working days by 8 (every working day is 8 hours long) with the number of workers and then sum them with the overtime. The working days equal 90% of the days that the firm has. The overtime equals the result of the multiplication of the number of workers by 2 (the possible hours of overtime) and then it is multiplied by the number of days that the firm has. From the task requirements, we see that the hours should be rounded down to the nearest integer, which we will do with the method Math.floor(…).

Checking The Conditions
After having done the calculations that are needed to find the value of the working hours, now we have to check whether these hours are enough, or some hours are left.
If the time is enough, we print the result that is specified in the task requirements, which in this case is the difference between the working hours and the hours needed for finishing the project.
If the time is not enough, we print the additional hours that are needed for finishing the project. They equal the difference between the hours for the project and the total working hours.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/930#4.