Chapter 7.1. Complex Loops
Since we have learned what for loops are and their function in code, now is the time to take a look at other loop types, as well as some more complex loop constructs. These will expand our knowledge and help us solve more challenging problems. In particular, we will discuss how to use the following programming constructs:
- loops with step
whileloopsdo-whileloops- infinite loops
In the current chapter, we will also take a look at the break operator and how to empty it to interrupt a loop.
Loops with a Step
In the "Loops (Repetitions)" chapter we learned how the for loop works and we already know when and to what purpose to use it. In the present chapter we will take a look at a particular and a very important part of this structure - its step.
Loop with a Step – Explanation
The step is the part of the for loop, that specifies the amount used to increment or decrement the main variable. The step is declared in the skeleton of the for loop.
Most often we have a size of 1 and in this case, instead of writing i += 1 or i -= 1, we can use the shorthand operators i++ or i--. In case we need the step to be different than 1 when increasing we use the shorthand i += + required step, and when we decrease i -= + required step. With a step of 3 the loop would appear as below:

Here is a series of sample problems, the solution of which will help us better understand the use of a step in a for loop.
Problem: Numbers 1...N with Step 3
Write a program that prints the numbers from 1 to n with a step of 3. For example, if n = 100, then the output would be: 1, 4, 7, 10, …, 94, 97, 100.
We can solve the problem using the following sequence of actions (algorithm):
- We create a function that will take the number
n. - We run a
forloop from 1 tonwith a step of 3. - in the body of the loop, we print the value of the current step.

Testing in The Judge System
You can test your solution at the following link: https://judge.softuni.org/Contests/Practice/Index/937#0.
Problem: Numbers N...1
Write a program that prints the numbers from n to 1 in reverse (step -1). For example, if n = 100, then the output will be: 100, 99, 98, …, 3, 2, 1.
We can solve the problem in the following manner:
- We create a function that will take the number
n. - We run a
forloop, by assigninglet i = n. - We reverse the condition of the loop:
i >= 1. - We define the step size: -1.
- in the body of the loop, we print the value of the current step.

Testing in The Judge System
You can test your solution at the following link: https://judge.softuni.org/Contests/Practice/Index/937#1.
Problem: Powers of Two
In the following example, we will use the standard size 1 step.
Write a program that prints the numbers from 1 to 2^n (two to the power of n). For example, if n = 10, then the output would be 1, 2, 4, 8, 16, 32, 64, 128, 256, 512, 1024.
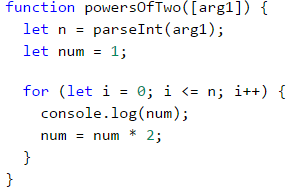
Testing in The Judge System
You can test your solution at the following link: https://judge.softuni.org/Contests/Practice/Index/937#2.
Problem: Even Powers of 2
Print the even powers of 2 until 2^n: 2^0, 2^2, 2^4, 2^8, …, 2^n. For example, if n = 10, then the output would be 1, 4, 16, 64, 256, 1024.
Here is how we can solve the problem:
- We create a function that will take the number
n. - We declare a variable
numthat will hold the current number and we assign it the initial value of 1. - For the step of the loop, we set a value of 2.
- In the body of the loop: we print the value of the current number and increase the current number
num4 times (as per the problem description).

Testing in The Judge System
You can test your solution at the following link: https://judge.softuni.org/Contests/Practice/Index/937#3.
While Loop
The next type of loops that we will familiarize are called while loops. The special thing about them is that they repeat a command block while a condition is met. Their structure is a bit different than that of the for loops, however, they boast a simpler syntax.
While Loop – Explanation
In programming, the while loop is used when we want to repeat the execution of a specific logic block until a specific condition is met. Any expression that returns either true or false (a Boolean) can be used as a "condition". When the condition becomes invalid, the while loop is interrupted and the program proceeds to execute the code after the loop. The while loop structure looks like this:

Here is a series of sample problems, the solutions of which will help us better understand the use of the while loop.
Problem: Sequence 2k+1
Write a program that prints all numbers ≤ n in the series: 1, 3, 7, 15, 31, …, assuming that each number is generated according to the following formula nextNumber = previousNumber * 2 + 1.
Here is how we can solve the problem:
- We create a function that will take the number
n. - We declare a variable
numthat will hold the current number and we assign it the initial value of 1. - For loop condition, we use the current number <= n.
- in the body of the loop: we print the value of the current number and increase the current number by using the formula above.
Here is a sample implementation of this idea:

Testing in The Judge System
You can test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#4.
Problem: Number in Range [1...100]
Enter an integer in the range [1 … 100]. If the entered number is invalid, enter another. In this case, an invalid number would be any number that is outside the given range.
To solve the problem, we can use the following algorithm:
- We declare variable
i, to which we assign the initial value of 0. Through which we save the position of each argument passed to our function. - We declare a variable
num, to which we assign the integer part of the first argument, passed to the function. - For a loop condition, we put a
trueexpression, if the number is not in the range specified in the problem description. - On the body of the loop: we increment
iso that at the next loop cycle we can take the next number passed to our function. We print the message "Invalid number!" on the console, afterwards we assign a new value tonum(the next argument, passed to our function). - Once we have validated the entered number, we print its value outside the body of the loop.
Here is a sample implementation of the algorithm using a while loop:

Testing in The Judge System
You can test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#5.
Greatest Common Divisor (GCD)
Before proceeding to the next problem, we should become familiar with the definition of the greatest common divisor (GCD).
Definition of GCD: the greatest common divisor of two natural numbers a and b is the largest number that divides both a and b without reminder. For example:
| a | b | GCD |
|---|---|---|
| 24 | 16 | 8 |
| 67 | 18 | 1 |
| 12 | 24 | 12 |
| 15 | 9 | 3 |
| 10 | 10 | 10 |
| 100 | 88 | 4 |
The Euclidean Algorithm
In the next problem we will use one of the first published algorithms for finding the GCD – Euclid's algorithm:
Until we have a remainder of 0:
- We divide the greater number by the smaller one.
- We take the remainder of the division.
Euclid's algorithm pseudo-code:
while b ≠ 0
var oldB = b;
b = a % b;
a = oldB;
print a;
Problem: Greatest Common Divisor (GCD)
Enter the integers a and b and find GCD(a, b).
We will solve the problem by implementing Euclid's algorithm:
- We declare variables
aandb, to which we assign the integer values, passed to our function. - For loop condition, we use a
trueexpression, if the numberbis different than 0. - In the body of the loop we follow the instructions from the pseudo-code:
- We create a temporary variable to which we assign the current value of
b. - We assign a new value to
b, which is the remainder of the division ofaandb. - On variable
awe assign the previous value of the variableb.
- We create a temporary variable to which we assign the current value of
- Once the loop is complete and we have found the GCD, we print it on the screen.

Testing in The Judge System
You can test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#6.
Do-While Loop
The next type of loop we will study is the do-while loop. By structure it resembles the while, but with a significant difference. The do-while will execute its body at least once. Why is this? In the do-while loop structure, the condition is always checked after the body, which ensures that the first loop iteration will execute the code and the check for the end of the loop will be applied to each subsequent iteration of the do-while.

Now we should proceed with the usual set of practical problems, that will help us better understand the do-while loop.
Problem: Factorial
For natural n number, calculate n! = 1 * 2 * 3 * … * n. For example, if n = 5, then the result would be: 5! = 1 * 2 * 3 * 4 * 5 = 120.
Here is how we can calculate factorial in more detail:
- We declare the variable
n, to which we assign the integer value, passed to our function. - We declare another variable -
fact, with an initial value of 1. We will use it in the calculation and store the factorial value. - For the loop condition we will use
n > 1, because each time we perform the calculations in the body of the loop, we will decrease the value ofnby 1. - In the body of the loop:
- We assign a new value to
fact, which value is the product of multiplying the currentfactwith the currentn. - We decrement
nwith 1.
- We assign a new value to
- Outside the body of the loop, we print the final factorial value.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#7.
Problem: Sum Digits
Sum up the digits of the integer positive number n. For example if n = 5634, then the output would be: 5 + 6 + 3 + 4 = 18.
We can use the following idea to solve the problem:
- We declare the variable
n, to which we assign a value equal to the number passed to our function. - We create a second variable -
sum, with an initial value of 0. We will use it for the calculation and storage of the result. - As a loop condition, we will use
n > 0, since, after each iteration of the loop, we will be removing the last digit fromn. - In the body of the loop:
- We assign a new value to
sum, which is the result of the sum of the current value ofsumwith the last digit ofn. - We assign a new value to
n, which is the result of removing the last digit ofn.
- We assign a new value to
- Outside the body of the loop, we print the final value of the sum.
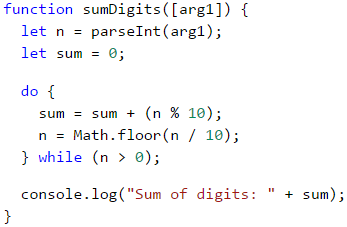
n % 10: returns the last digit of the number n.Math.floor(n / 10): deletes the last digit of n. |
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#8.
Infinite Loops and The break Operator
So far, we were introduced to various types of loops, learning what structures they have and how they are applied. Now, we need to understand what an infinite loop is, when it occurs, and how we can break it using the break operator.
Infinite Loop – Explanation
An infinite loop runs infinitely the execution of its body. With while and do-while loops the end check is a conditional expression that always returns true. Infinite for occurs when there is no condition to end the loop.
Here is an example of an infinite while loop:
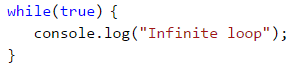
And here is an infinite for loop:

The break Operator
We already know that the infinite loop executes a certain code infinitely, but what if we want at some point under a given condition to interrupt and exit the loop? The break operator comes in handy in this situation.
The operator break stops a loop's execution at the point it is called and the execution continues from the first line after the end of the loop. This means that the current iteration of the loop will not be completed accordingly and the rest of the code in the body of the loop will not be executed. |
Problem: Check Prime
The next problem we are going to solve is to check whether a given number is prime, but before that, we should remember what are prime numbers.
Definition: An integer is considered prime if it is divisible only by itself and by 1. By definition, the prime numbers are positive and greater than 1. The smallest prime number is 2.
We can assume that an integer n is a prime number if n > 1 and n is not divisible by a number between 2 and n-1.
The first few prime numbers are: 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43, …
By contrast, composite numbers are integers, which can be obtained by multiplying several prime numbers.
Here are some examples of composite numbers:
- 10 = 2 * 5
- 42 = 2 3 7
- 143 = 13 * 11
An algorithm to check whether a given number is prime: we check if n > 1 and if n is divisible by 2, 3, …, n-1 without remainder.
- If it is divisible by any of the numbers, it is composite.
- If it is not divisible by any of the numbers, then it is prime.
We can optimize the algorithm by instead of checking until n-1, checking divisors only until √n. Think of the reasons why this is so. |
Problem: Enter Even Number
You are tasked to write a function that takes a single input n integer and checks if it is prime. This can be implemented by checking if n is divisible by any numbers in the range between 2 and √n.
The steps of the "prime checking algorithm" are given below in bigger detail:
- We declare the variable
n, to which we assign the integer passed to our function. - We create a
primeboolean with, and an initial value oftrue. We assume that a number is prime until proven otherwise. - We create a
forloop, with the initial value set to 2, for a condition the current value<= √n. The step is set to 1. - In the body of the loop, we check if
n, divided by the current value has a remainder. If there is no reminder from the division, then we changeprimetofalseand exit the loop through thebreakoperator. - Depending on the value of
primewe print whether the input number is prime (true) or composite (false).
Here is a sample implementation of the prime checking algorithm, described above:

What remains is to add a condition that checks if the input number is greater than 1, because, by definition numbers such as 0, 1, -1, and -2 are not prime.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#9.
Problem: Break Sum
Write a function, which checks whether a given number n is even and if so - print it on the console. An even number can be divided by 2 without a remainder. If the number is invalid, we will print that the current number is not even and the user will need to input a new number.
Here is an idea for the solution:
- We declare the variable
i, which shall hold the initial value of 0. Through it, we will store the position of every number passed to our function. - We declare a variable
num, with an initial value of 0. - We create an infinite
whileloop with a condition set totrue. - In the body of the loop:
- We take the integer value, passed to our function, and assign it to
num. - If the number is even, we exit the loop by a
break. - Otherwise, we print a message stating that the number is not even. We increment
iso that we can take the next number from the input on the next iteration. The iterations continue until an even number is entered.
- We take the integer value, passed to our function, and assign it to
- We print the even number on the console.
Here is an example implementation of the idea:
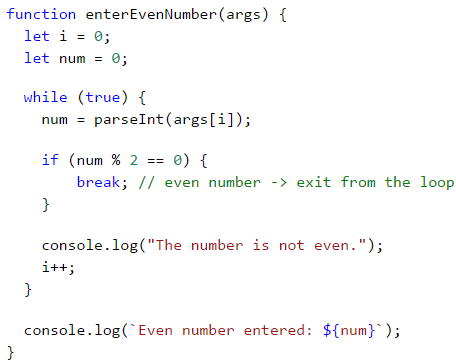
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#10.
Nested Loops and The break Operator
Now since we know what the nested loops are and how the break operator works, it is time to figure out how they work together. To get a better idea, we should write a function step by step, that should make all possible combinations of number pairs. The first number in the pair is increasing from 1 to 3, while the second one is decreasing from 3 to 1. Our solution must continue running until i + j is not equal to 2 (i.e. i = 1 and j = 1).
The desired result is:
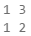
Here is a wrong implementation, that looks right at first glance:

If we leave our function that way, our result will be as follows:
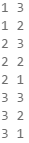
Why is this so? As we can see, the result is missing "1 1". When the function reaches the point when i = 1 and j = 1, it enters the if check and executes the break operation. This way, it exits the inner loop, but then continues the execution of the outer loop. i increases, the function enters the inner loop and prints the result.
When we use the break operator in a nested loop, it interrupts only the execution of the inner loop. |
What is the correct solution? One way to solve the problem is by declaring a bool variable, to keep track if the loop iteration has to continue. If we have to exit (leave all nested loops), we set the variable to true and exit the inner loop with break and in the next check, we exit the outer loop. Here is an example implementation of this idea:

In this manner, when i + j = 2, the program will set the variable hasToEnd = true and will exit the inner loop. Upon the next iteration of the outer loop, via the if check, the function will not reach the inner loop and will interrupt its execution.
Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#11.
Exercises with loops
In this chapter, we got familiar with a few new types of loops that can perform repetitions with more complex programming logic. Let's solve a few practical problems using these new constructs.
Problem: Fibonacci
Fibonacci's numbers in mathematics form a sequence that looks like this: 1, 1, 2, 3, 5, 8, 13, 21, 34, ….
The formula to derive the next member of Fibonacci's sequence is:
F0 = 1
F1 = 1
Fn = Fn-1 + Fn-2
Sample Input and Output
| Input (n) | Output | Comment |
|---|---|---|
| 10 | 89 | F(11) = F(9) + F(8) |
| 5 | 8 | F(5) = F(4) + F(3) |
| 20 | 10946 | F(20) = F(19) + F(18) |
| 0 | 1 | |
| 1 | 1 |
Enter an integer number n and calculate the n-th Fibonacci number.
Hints and Guidelines
An idea to solve the problem:
- We declare a variable
n, which will hold the integer value passed to our function. - We create the variables
f0andf1, to which we assign the value to 1 since this is the start of Fibonacci's sequence. - We create a
forloop with condition current valuei < n - 1. - In the body of the loop:
- We create a temporary variable
fNext, to which we assign the next number in the Fibonacci sequence. - To
f0we assign the current value off1. - To
f1we assign the value of the temporary variablefNext.
- We create a temporary variable
- Out of the loop we print the n-th number of Fibonacci.
Example implementation:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#12.
Problem: Number Pyramid
Print the numbers 1 … n in a pyramid as per the below example. On the first row, we print one number, at the second we print two, at the third, we print three, and so on, until the numbers are over. On the last line, we print as many numbers as we get until we get to n.
Sample Input and Output
| Input | Output | Input | Output | Input | Output |
|---|---|---|---|---|---|
| 7 | 1 2 3 4 5 6 7 |
5 | 1 2 3 4 5 |
10 | 1 2 3 4 5 6 7 8 9 10 |
Hints and Guidelines
We can solve the problem with two nested loops (by rows and columns) by printing in them and leaving when the last number is reached. Here is the idea, written in more detail:
- We declare a variable
n, to which we assign the integer value passed to our function. - We declare a variable
numwith an initial value of 1. It will hold the count of printed numbers. At each iteration, we will increment it by 1 and will add it to the current row. - We declare a variable
result, which will hold the current row and to which we will add the value of the current cell. - We create an outer
forloop, which will be responsible for the rows in the table. The loop variable will be namedrowand we assign it an initial value of 1. For condition, we setrow < n. The step will also be 1. - In the body of the loop, we create an inner
forloop, which will be responsible for the columns in the table. We name the variablecoland assign it an initial value of 1. For condition we setcol < row(row= number of digits per line). The step will also be 1. - In the body of the nested loop:
- We check whether
col > 1, if true we add a space to the variableresult. If we do not make this check and instead add the space every time, each resulting line will start with a space. - We store the number
numin the current cell of the table and increment it by 1. - We check if
num > n. If thenumis greater thann, we interrupt the inner loop.
- We check whether
- We print the value of the variable
resultand after that, we set it to an empty value. This way we can proceed to the next line. - Again, we check if
num > n. If it is greater, we interrupt the execution of our function with abreak.
Here is an example implementation:

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#13.
Problem: Number Table
Print the numbers 1 … n in a table as per the examples below:
Sample Input and Output
| Input | Output | Input | Output |
|---|---|---|---|
| 3 | 1 2 3 2 3 2 3 2 1 |
4 | 1 2 3 4 2 3 4 3 3 4 3 2 4 3 2 1 |
Hints and Guidelines
We can solve the problem by using two nested loops and some simple calculations in them:
- We take the size of the table from the integer value of the variable
n, which is passed to our function. - We declare the variable
result, which will hold the current row and to which we will add the value of the current cell. - We create a
forloop, that will be responsible for the rows of the table. We name the loop variablerowand assign it an initial value of 0. For condition, we setrow < n. The size of the step is 1. - In the body of the loop we create a nested
forloop, that will be responsible for the columns in the table. We name the loop variablecoland assign it an initial value of 0. For condition, we setcol < n. The size of the step is set to 1. - In the body of the nested loop:
- We create a variable
num, to which we assign the result of the current row + the current column + 1 (+1 is needed since we count from 0). - We check whether
num > n. Ifnumis greater thann, we assignnuma new value equal to two timesn- the current value ofnum. We do this in order not to exceedn** in any of the cells of the table. - We add the number of the current cell to the variable
result.
- We create a variable
- We print the value of the result, after which we set it to a new empty value. This way we can proceed to the next line.

Testing in The Judge System
Test your solution here: https://judge.softuni.org/Contests/Practice/Index/937#14.
What Have We Learned from This Chapter?
We can use for loops with a step:
for (let i = 1; i <= n; i+=3) {
console.log(i);
}
The while / do-while loops are repeated while a condition is true:
let num = 1;
while (num <= n) {
console.log(num++);
}
If we have to interrupt the loop execution, we use the break operator:
let n = 0;
while (true) {
n = parseInt(arg1);
if (n % 2 === 0) {
break; // even number -> exit from the loop
}
console.log("The number is not even.");
}
console.log(`Even number entered: ${num}`);